In previous articles in this Time Series with Tensorflow series we've built simple dense models, a CNN, an LSTM, and used both univariate and multivariate data as inputs for forecasting the price of Bitcoin.
In this article, we'll expand on these previous models and replicate the N-BEATS algorithm, which stands for:
Neural basis expansion analysis for interpretable time series forecasting
As the paper states, the algorithm is focused on:
...solving the univariate times series point forecasting problem using deep learning.
There are a few reasons to replicate this algorithm, specifically:
- It will allow us to practice replicating a paper with TensorFlow code
- We will see how to use TensorFlow layer subclassing to make our own custom layers
- We will get experience using the Functional API to create a custom architecture
- And of course, potentially get state-of-the-art results on our forecasting problem
This article is based on notes from this TensorFlow Developer Course and is organized as follows:
- Replicating N-BEATS in TensorFlow
- Testing our N-BEATS block implementation
- Preparing data for the N-BEATS algorithm using tf.data
- Making our dataset performant using the tf.data API
- Setting hyperparameters for the N-BEATS algorithms
- Steps we need to take to build the N-BEATS model
- Building, fitting and compiling the N-BEATS algorithm
- Evaluating the N-BEATS results
- Plotting the N-BEATS algorithm
Subscribe now
Replicating N-BEATS in TensorFlow
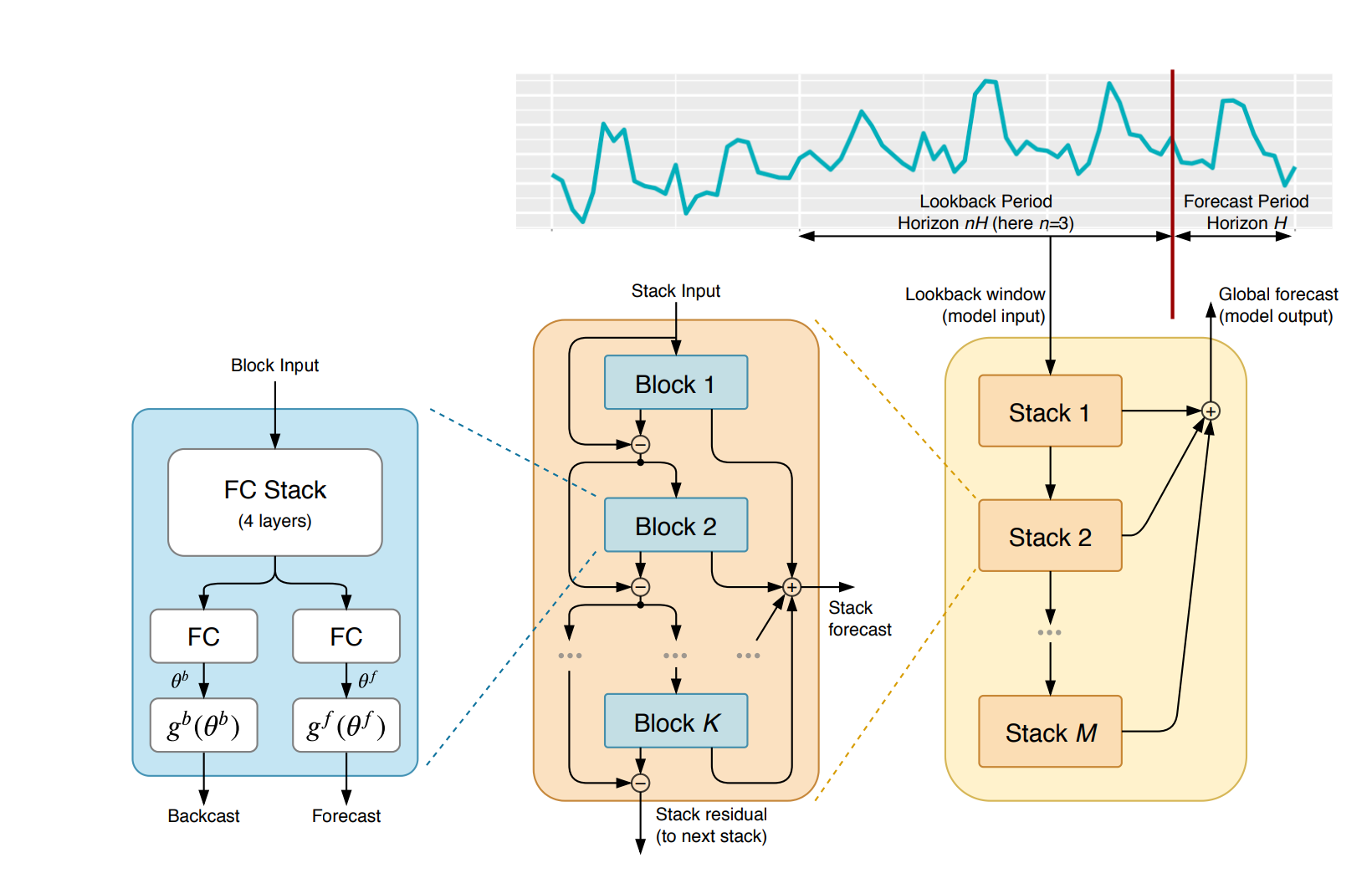
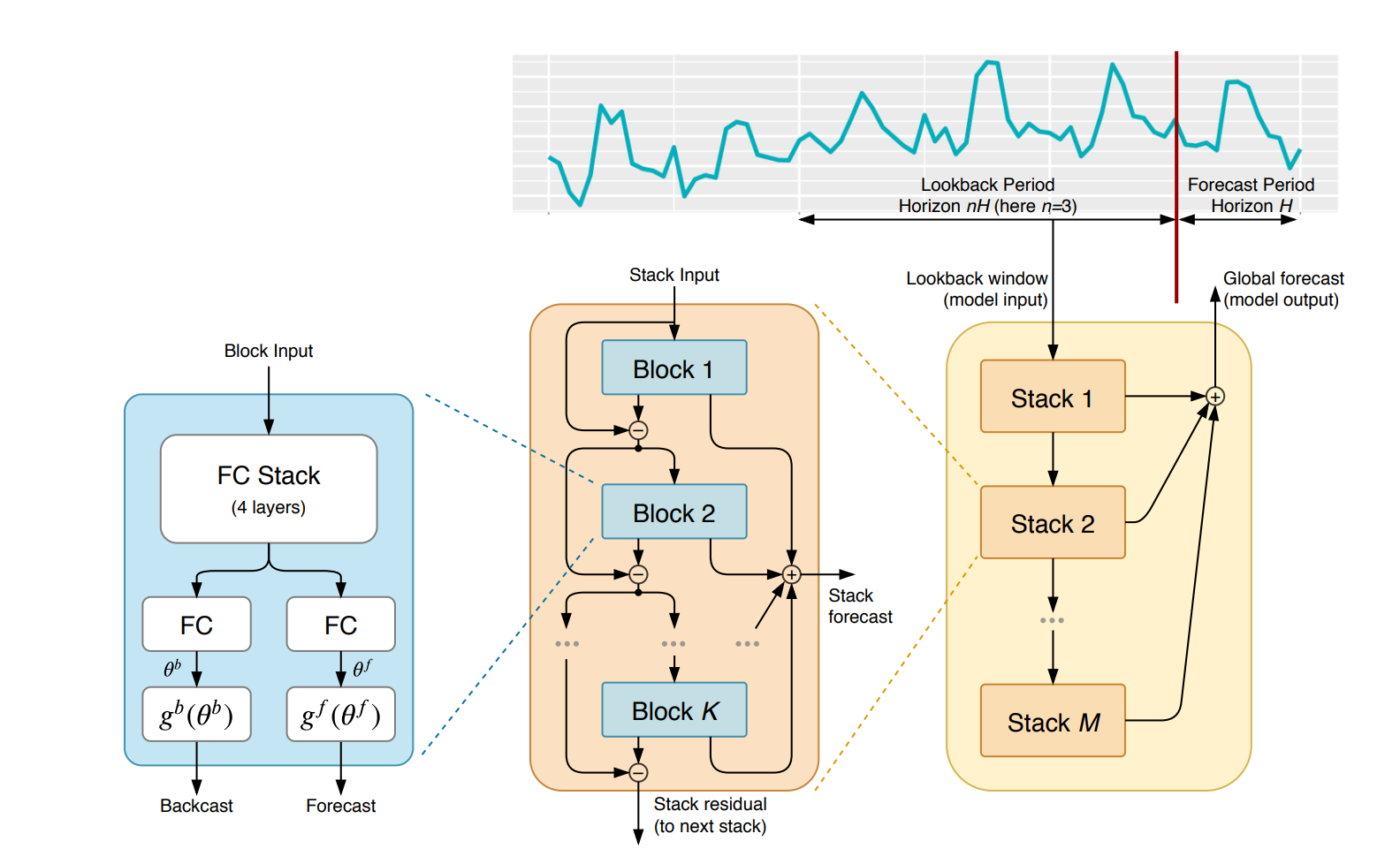
To start, let's begin by replicating the block input from the figure below. As the paper states:
The basic building block is a multi-layer FC network with ReLu nonlinearities. It predicts basis expansion coefficients both forward, $θ^f$, (forecast) and backward, $θ^b$, (backcast).
To do so, we first need to create a custom layer subclass called NBeatsBlock. You can learn more about making new layers and models via subclassing with TensorFlow here.
The reason we need to create this custom layer is that N-BEATS block layer doesn't exist in TensorFlow.
The two methods we need to introduce in our layer is the constructor and a call method.
First, let's start by outlining the __init__ method below (we'll fill in the specific integers later):
# Create N-BEATS custom layer
class NBeatsBlock(tf.keras.layers.Layer):
def __init__(self,
input_size: int,
theta_size: int,
horizon: int,
n_neurons: int,
n_layers: int,
**kwargs): # The **kwargs argument takes care of all the arguments for the parent class
super().__init__(**kwargs)
self.input_size = input_size
self.theta_size = theta_size
self.horizon = horizon
self.n_neurons = n_neurons
self.n_layers = n_layersNext, we need to create a stack of 4 fully connected (i.e. dense) layers with ReLu non-linearities. Specifically, we need to recreate the "Block Input" from the image above as follows:
- The block contains a stack of 4 fully connected layers and each has ReLU activation
- Output of the block is a theta layer with linear activation
- We then need a
callmethod as all TensorFlow subclass layers require one, which is the operation the layer will perform when we call it in a model.
# Create N-BEATS custom layer
class NBeatsBlock(tf.keras.layers.Layer):
def __init__(self,
input_size: int,
theta_size: int,
horizon: int,
n_neurons: int,
n_layers: int,
**kwargs): # The **kwargs argument takes care of all the arguments for the parent class
super().__init__(**kwargs)
self.input_size = input_size
self.theta_size = theta_size
self.horizon = horizon
self.n_neurons = n_neurons
self.n_layers = n_layers
# Block contains stack of 4 fully connected layers, each has ReLU activation
self.hidden = [tf.keras.layers.Dense(n_neurons, activation='relu') for _ in range(n_layers)]
# Output of the block is a theta layer with linear activation
self.theta_layer = tf.keras.layers.Dense(theta_size, activation="linear", name="theta")
def call(self, inputs):
x = inputs
for layer in self.hidden:
x = layer(x)
theta = self.theta_layer(x)
# Output the backcast and forecast from theta
backcast, forecast = theta[:, :self.input_size], theta[:, -self.horizon:]
return backcast, forecastTesting our N-BEATS block implementation
Now that we've recreated the N-BEATS basic block with a TensorFlow subclass, let's test the NBeatsBlock and see what the inputs and outputs might look like with dummy data.
Below we'll use the generic hyperparameters from the paper:
# Set up dummy NBeatsBlock layer to represent inputs and outputs
dummy_nbeats_block_layer = NBeatsBlock(input_size=WINDOW_SIZE,
theta_size=WINDOW_SIZE+HORIZON, # backcast + forecast
horizon=HORIZON,
n_neurons=128,
n_layers=4)Next, we'll create out dummy inputs and outputs as follows:
dummy_inputs = tf.expand_dims(tf.range(WINDOW_SIZE) + 1, axis=0) # input shape to the model has to reflect dense layer input requirements (ndim=2)Now let's pass the dummy_inputs through our instance of the dummy_nbeats_block_layer. Note the outputs will be random since the model isn't trained:
# Pass dummy inputs to dummy NBeatsBlock layer
backcast, forecast = dummy_nbeats_block_layer(dummy_inputs)
# These are the activation outputs of the theta layer
print(f"Backcast: {tf.squeeze(backcast.numpy())}")
print(f"Forecast: {tf.squeeze(forecast.numpy())}")
We now have our window dummy data being passed through the block input and outputting a backcast and a forecast.
Next, we'll discuss how we're going to prepare our data for the N-BEATS algorithm with the tf.data API.
Preparing data for the N-BEATS algorithm using tf.data
Let's now prepare our data for the N-BEATS algorithm. Given that it will be a much larger neural network than previous models in this series, we're going to use the tf.data API, which as the docs say:
The tf.data API enables you to build complex input pipelines from simple, reusable pieces.A key part of a Machine Learning Engineer's job when building larger neural networks is making sure your data input pipeline is as performant as possible.
In order to make our input data load as possible, we'll be following the performant data pipeline steps in the tf.data docs.
The first step is to instantiate our window and horizon sizes for the dataset:
# Setup dataset hyperparameters
HORIZON = 1
WINDOW_SIZE = 7Next, we'll create the N-BEATS data inputs, which as mentioned works with univariate time series data. To recap, in the project we're working with Bitcoin price data in order to forecast future prices:
bitcoin_prices.head()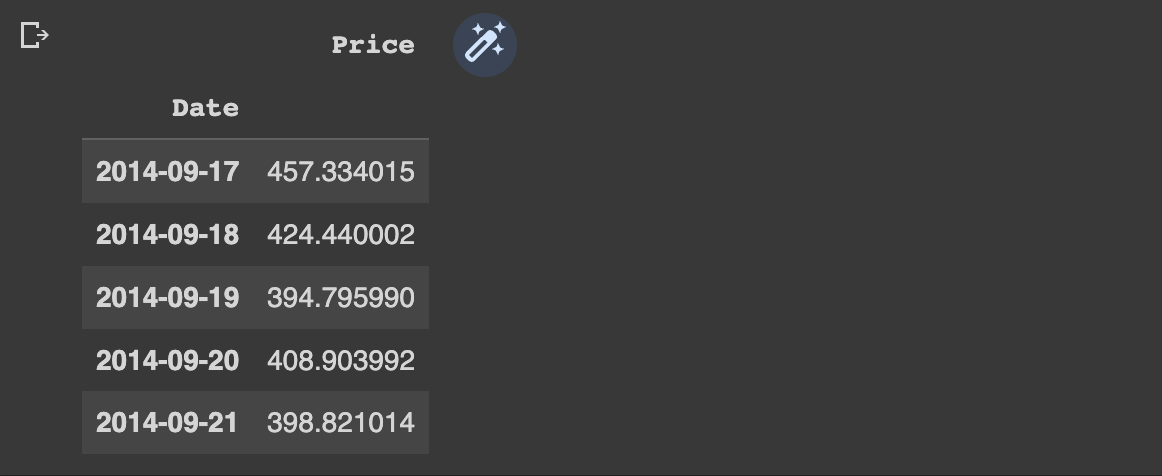
First, we'll create windowed columns of our bitcoin price data using Pandas:
# Add windowed columns
bitcoin_prices_nbeats = bitcoin_prices.copy()
for i in range(WINDOW_SIZE):
bitcoin_prices_nbeats[f"Price+{i+1}"] = bitcoin_prices_nbeats["Price"].shift(periods=i+1)
bitcoin_prices_nbeats.head()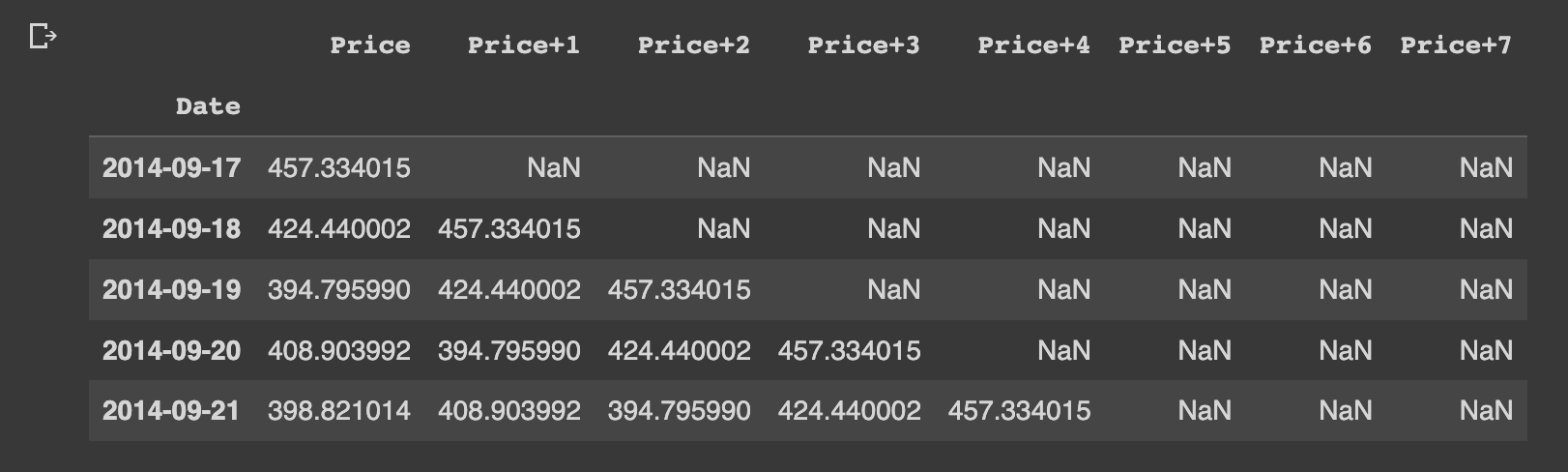
Next, we'll get rid of the NaN numbers, make our features and labels, and then make train and test splits:
# Make features and labels
X = bitcoin_prices_nbeats.dropna().drop("Price", axis=1)
y = bitcoin_prices_nbeats.dropna()["Price"]
# Make train and test sets
split_size = int(len(X) * 0.8)
X_train, y_train = X[:split_size], y[:split_size]
X_test, y_test = X[split_size:], y[split_size:]
len(X_train), len(y_train), len(X_test), len(y_test)Now that we've got arrays of training data, testing data, windows, and horizons, let's make them performant wiht the tf.data API.
Making our dataset performant using the tf.data API
First, we'll create a features dataset using tf.data.Dataset.from_tesnor_slices(), then a labels dataset, and then we'll do the same with the test dataset:
# Let's make our dataset performant using tf.data API
train_features_dataset = tf.data.Dataset.from_tensor_slices(X_train)
train_labels_dataset = tf.data.Dataset.from_tensor_slices(y_train)
test_features_dataset = tf.data.Dataset.from_tensor_slices(X_test)
test_labels_dataset = tf.data.Dataset.from_tensor_slices(y_test)Next, we're going to combine features and labels by zipping them together into a tuple for both the train and test sets:
# Combine labels and features by zipping together -> (features, labels)
train_dataset = tf.data.Dataset.zip((train_features_dataset, train_labels_dataset))
test_dataset = tf.data.Dataset.zip((test_features_dataset, test_labels_dataset))Next, we have to batch and prefetch the data as follows:
# Batch and prefetch
BATCH_SIZE = 1024
train_dataset = train_dataset.batch(BATCH_SIZE).prefetch(tf.data.AUTOTUNE)
test_dataset = test_dataset.batch(BATCH_SIZE).prefetch(tf.data.AUTOTUNE)Looking at our train and test data, we now have a prefetched dataset and a tuple:

The next step before using the model is to set the hyperparameters for the N-BEATS algorithm.
Setting hyperparameters for the N-BEATS algorithms
Let's now set set up hyperparameters for the N-BEATS algorithm.
The hyperparamaters that we'll be setting up can all be found in Table 18 of the N-BEATS paper:
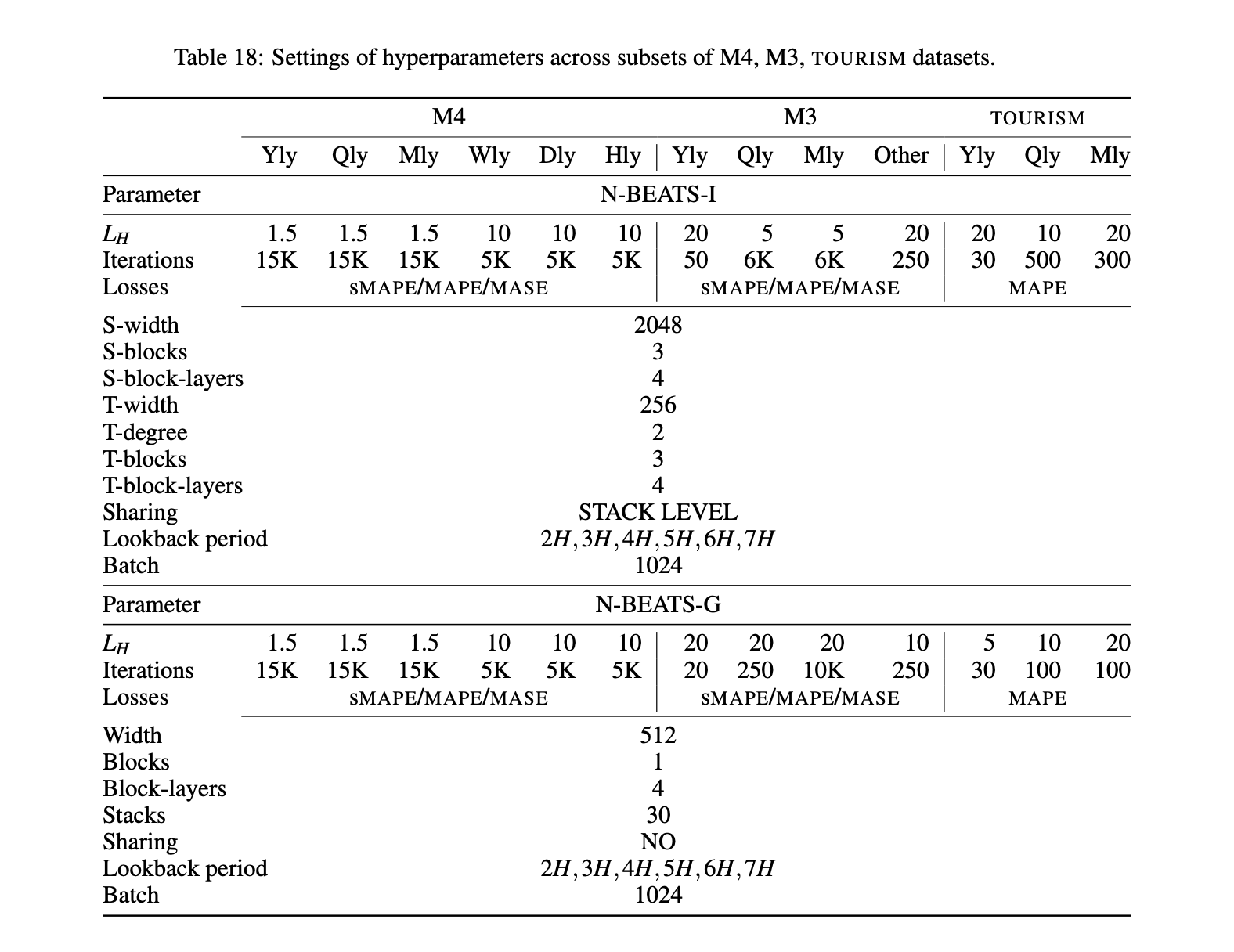
The ones we will use can be found in the daily column, and the N-BEATS-G section:
N_EPOCHS = 5000
N_NEURONS = 512
N_LAYERS = 4
N_STACKS = 30
INPUT_SIZE = WINDOW_SIZE * HORIZON
THETA_SIZE = INPUT_SIZE + HORIZONPreparing for residual connections
There's one more step before we're ready to put everything together: we need to get ready for residual connections.
If we look at section 3.2 of the paper they refer to this as "Doubly Residual Stacking", which is:
The classical residual network architecture adds the input of the stack of layers to its output before passing the result to the next stack (He et al., 2016)...We propose a novel hierarchical doubly residual topology depicted in Fig. 1 (middle and right). The proposed architecture has two residual branches, one running over backcast prediction of each layer and the other one is running over the forecast branch of each layer.
This is represented in the middle section of the model architecture:
Let's now prepare the code for the two layers we'll need for residual connections with two dummy tensors:
# Make tensors
tensor_1 = tf.range(10) + 10
tesnor_2 = tf.range(10)
# Subtract
subtracted = layers.subtract([tensor_1, tensor_2])
# Add
added = layers.add([tensors_1, tensor_2])Steps we need to take to build the N-BEATS model
We now have the building blocks we need to replicate the N-BEATS algorithm, let's outline the steps we need to take.
The steps we need to take include:
- Setup and instance of the N-BEATS block layer using the
NBeatsBlockclass we created. This will be the initial block used for the network, and the rest will be created as part of stacks. - Create an input layer for the N-BEATS stack (we'll be using the Keras Functional API)
- Make the initial backcast and forecast for the model with the layer created in (1)
- Use for loop to create stacks of block layers
- Use the
NBeatsBlockclass within the for loop in (4) to create blocks that return backcasts and block-level forecasts - Create the double residual stacking using subtract and add layers
- Put the model inputs and outputs together using
tf.keras.Model() - Compile the model with MAE loss (the paper uses multiple losses, but we'll use MAE to keep in inline with other models) and Adam optimizer with default settings as per section 5.2 of the paper
- Fit the N-BEATS model for 5000 epochs—we'll use several callbacks since we're training for so long including "early stopping" (i.e. if it stops improving) and "reduce LR on plateau" (i.e. if a model stops improving, try lowering the learning rate)
Building, fitting, and compiling the N-BEATS algorithm
We're now ready to put everything together and start implementing the N-BEATS algorithm with the steps above.
First, let's set up an instance of the N-BEATS block:
%%time
tf.random.set_seed(42)
# 1. Setup an instance of N-BEATS block
nbeats_block_layer = NBeatsBlock(input_size=INPUT_SIZE,
theta_size=THETA_SIZE,
horizon=HORIZON,
n_neurons=N_NEURONS,
n_layers=N_LAYERS,
name='InitialBlock')Next, we'll create an input to stack:
# 2. Create an input to stack
stack_input = layers.Input(shape=(INPUT_SIZE), name='stack_input')For step 3 we will make an initial backcast and forcest for the model:
# 3. Create initial backcast and forecast (backwards prediction + horizon prediction)
residuals, forecast = nbeats_block_layer(stack_input)Next, we'll create a stack of block layers and then we'll use the NBeatsBlock to calculate the backcast and forecast:
# 4. Create stacks of block layers
for i, _ in enumerate(range(N_STACKS-1)): # first stack is already created in #3
# 5. Use the NBeatsBlock to calculate the backcast and forecast
backcast, block_forecast = NBeatsBlock(
input_size=INPUT_SIZE,
theta_size=THETA_SIZE,
horizon=HORIZON,
n_neurons=N_NEURONS,
n_layers=N_LAYERS,
name=f"NBeatsBlock_{i}"
)(residuals) # pass in the residualsNext, we'll create the double residual stacking using subtract and add layers inside the for loop we just created:
# 6. Create double residual stacking
residuals = tf.keras.layers.subtract([residuals, backcast], name=f"subtract_{i}")
forecast = tf.keras.layers.add([forecast, block_forecast], name=f"add_{i}")The next step is to put the model inputs and outputs together using tf.keras.Model():
# 7. Put the stack model together
model_7 = tf.keras.Model(inputs=stack_input, outputs=forecast, name="model_7_NBEATS")Next, we'll compile the model with MAE loss:
# 8. Compile model with MAE loss
model_7.compile(loss="mae",
optimizer=tf.keras.optimizers.Adam()) The last step is to fit the model for 5000 epochs with callbacks:
# 9. Fit the model wiht EarlyStopping and ReduceLRonPlateau callabcks
model_7.fit(train_dataset,
epochs=N_EPOCHS,
validation_data=test_dataset,
verbose=0,
callbacks=[tf.keras.callbacks.EarlyStopping(monitor="val_loss",
patiences=200,
restore_best_weights=True),
tf.keras.callbacks.ReduceLRonPlateau(monitor='val_loss',
patience=100,
verbose=1)])Let's now run the model for 5000 epochs and evaluate the results.
Evaluating the N-BEATS results
It doesn't look like our model reached the full 5000 epochs because of the callbacks, but regardless, we're now ready to evaluate the results on the test dataset.
# Evaluate N-BEATS model on the test dataset
model_7.evaluate(test_dataset)# Make predictions with the N-BEATS model
model_7_preds = make_preds(model_7, test_dataset)
model_7_preds[:10]# Evaluate N-BEATS model preds
model_7_results = evaluate_preds(y_true=y_test,
y_pred=model_7_preds)
model_7_results
Comparing this to our naive results:
naive_results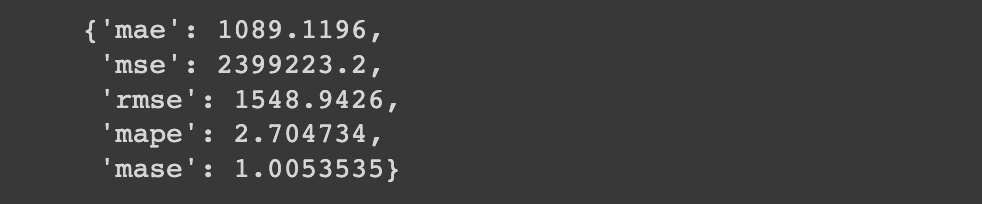
Despite replicating the cutting-edge N-BEATS algorithm, we still see it's performing worse than our simplest model.
One thing we can see is that all of our models are getting similar results, which may tell us something about the underlying data...we'll get to that point a bit later.
This also tells us that, especially with a difficult task like time series forecasting, just because you can build a deep learning model, doesn't mean you always should.
Plotting the N-BEATS algorithm
Before we finish, let's plot the N-BEATS implementation we've created.
To do so, we're going to use the plot_model method from TensorFlow:
# Plot the N-BEATS
from tensorflow.keras.utils import plot_model
plot_model(model_7)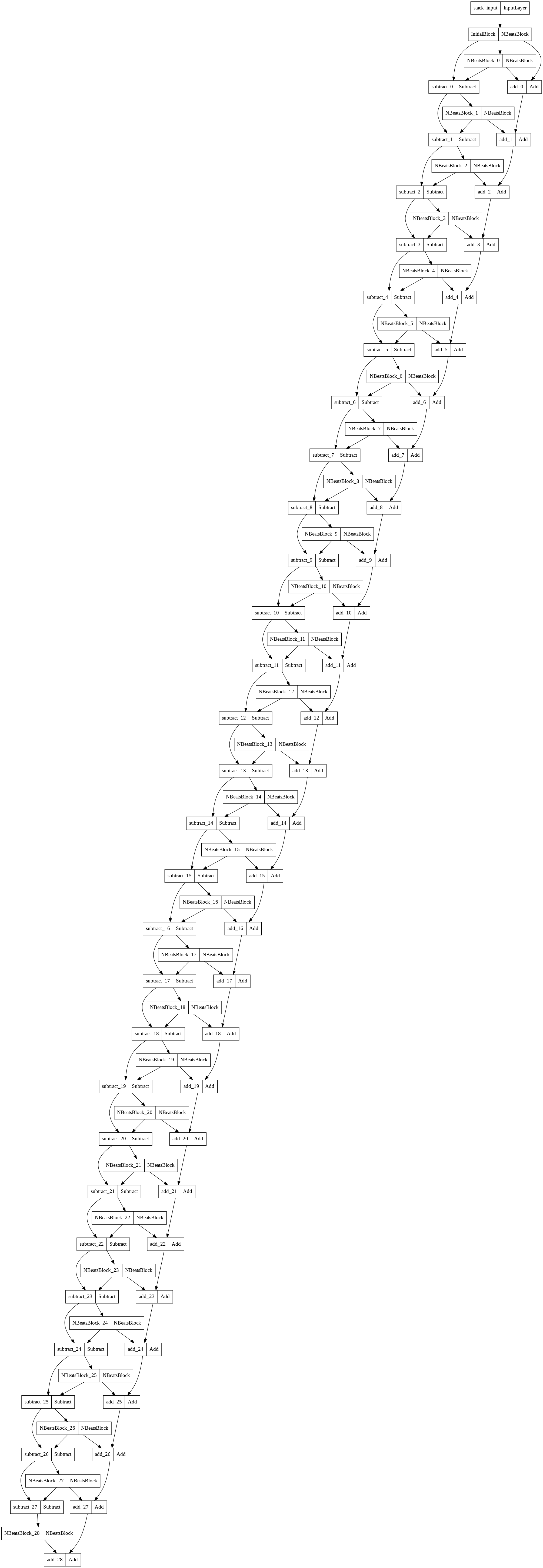
Quite impressive...
Summary: Replicating the N-BEATS algorithm
The article discussed how to replicate the N-BEATS algorithm in TensorFlow for time series forecasting.
- The N-BEATS algorithm is a deep learning approach to solving the univariate times series point forecasting problem.
- The steps to replicate the algorithm in TensorFlow include creating a custom NBeatsBlock layer and using the tf.data API for data preparation.
- The article also covered setting hyperparameters and building, fitting, and compiling the N-BEATS algorithm, as well as evaluating and plotting results.
As we saw, even with all these layers we still weren't able to beat the results of our naive model.
Of course, there are many more steps we could take to improve the results of our N-BEATS implementation, but for now, we're going to move on to building an ensemble machine learning model for time series forecasting in the next article.






