Quantum Machine Learning: Introduction to TensorFlow Quantum

Released in March 2020 by Google, TensorFlow Quantum (TFQ) is a:

quantum machine learning library for rapid prototyping of hybrid quantum-classical ML models.

The library integrates quantum computing algorithms and logic designed in Google Cirq, and is compatible with existing TensorFlow APIs.

In this introductory guide we'll assume you have some knowledge of TensorFlow, Cirq, and quantum machine learning, although if you need a refresher in any of these topics check out these articles:

The following article is based on notes from the tutorials and paper provided by TFQ, and is organized as follows:

Overview of TensorFlow Quantum
TensorFlow Quantum Architecture
Quantum Machine Learning Pipeline with TFQ
TensorFlow Quantum Primitives
Hello, Many Worlds
Quantum Machine Learning with TFQ: Tutorials

1. Overview of TensorFlow Quantum

As mentioned in the TensorFlow Quantum tutorial:

TensorFlow Quantum focuses on quantum data and building hybrid quantum-classical models. It provides tools to interleave quantum algorithms and logic designed in Cirq with TensorFlow.

As a refresher, Google's Cirq framework is:

A python framework for creating, editing, and invoking Noisy Intermediate Scale Quantum (NISQ) circuits.

Hybrid Quantum-Classical Models

Since near-term quantum processors are relatively small and noisy, quantum models cannot generalize quantum data solely using quantum processors. Instead, Noisy Intermediate Scale Quantum (NISQ) processors work together with classical processors to be useful. TensorFlow Quantum is used as a base platform to experiment with hybrid quantum-classical algorithms.

TensorFlow Quantum is built for solving NISQ-era quantum machine learning problems. It combines quantum computing primitives —such as building quantum circuits—with the TensorFlow ecosystem.

Cirq & TensorFlow Quantum

As discussed in our article on Quantum Programming with Google Cirq, Cirq is a quantum programming framework that provides basic operations such as qubits, gates, circuits, and measurement.

As described in their article on the design of TensorFlow Quantum:

TensorFlow Quantum uses these Cirq primitives to extend TensorFlow for batch computation, model building, and gradient computation. To be effective with TensorFlow Quantum, it’s a good idea to be effective with Cirq.

2. TensorFlow Quantum Architecture

In order to avoid certain technical hurdles associated with combing TensorFlow and Cirq, the TFQ paper describes the following four design principles:

Differentiability: Since gradient-based methods that leverage autodifferentiation have become the leading optimization technique in traditional machine learning, TFQ must support differentiation of quantum circuits so that hybrid quantum-classical models can participate in backpropagation.
Circuit Batching: The QML framework must be optimized for running large numbers of parameterized model circuits on each quantum data point.
Execution Backend Agnostic: The framework allows users to switch between running models in simulation and models on real hardware, so that the two can be directly compared.
Minimalism: Existing functionality in Cirq and TensorFlow should be used as much as possible. TFQ should only serve as a bridge between the two and not require users to re-learn how to solve problems with quantum computing or machine learning.

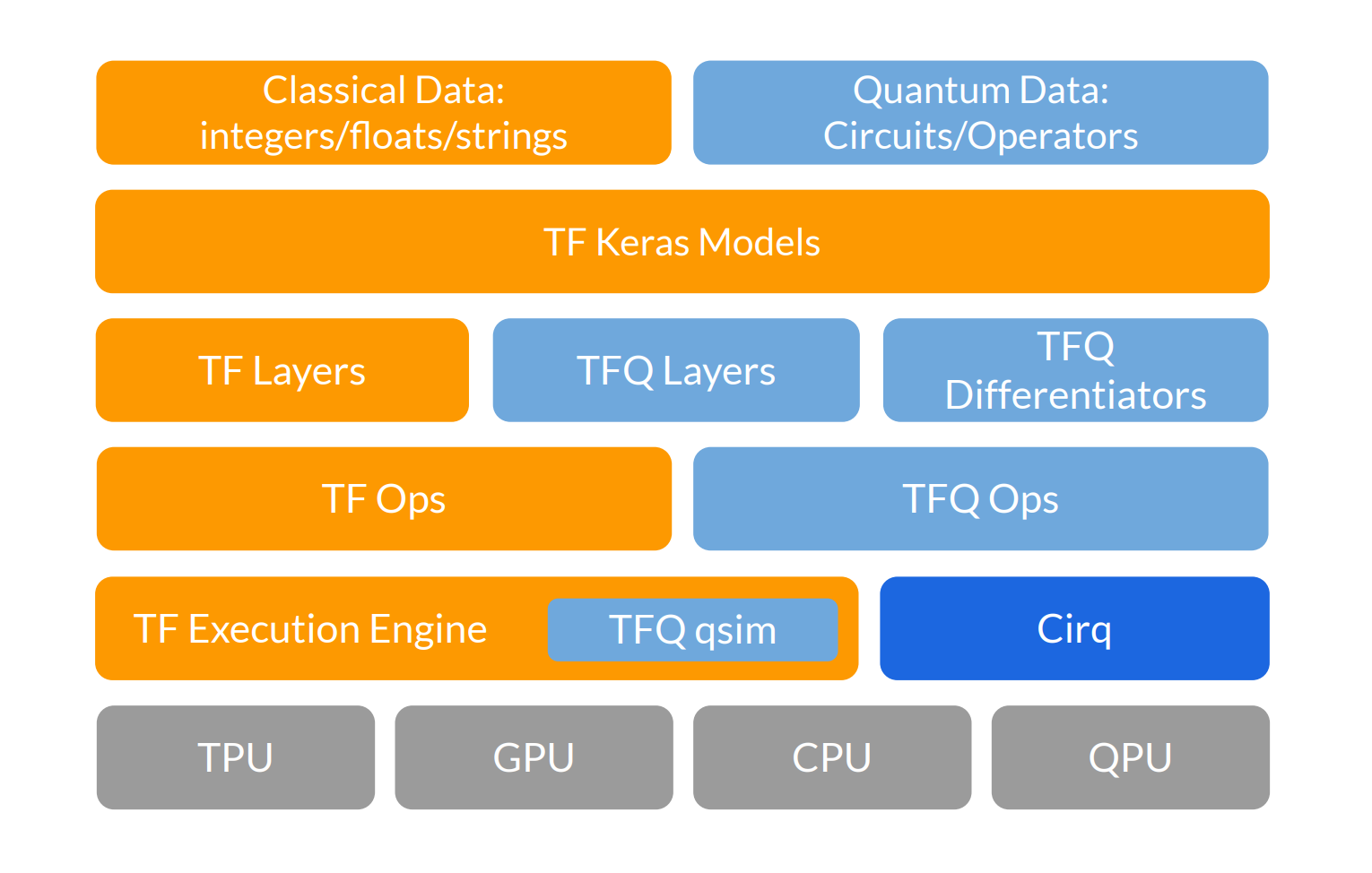
Below we can see the software stack of TFQ, including its interaction with TensorFlow, Cirq, and computational hardware. We can see that classical data is processed with TensorFlow, and TFQ adds the ability to process quantum data.

The next layer is the Keras API, which psans the full width of the stack. Below that we have TensorFlow layers, quantum layers, and differentiators, which enable hybrid quantum-classical automatic differentiation. Next we have TensorFlow Ops, which instantatiate the dataflow graph. TFQ Ops controsl the quantum circuit execution. The circuits can be executed in simulation with qsim or Cirq, and eventually with QPU hardware.

source

3. Quantum Machine Learning Pipeline with TFQ

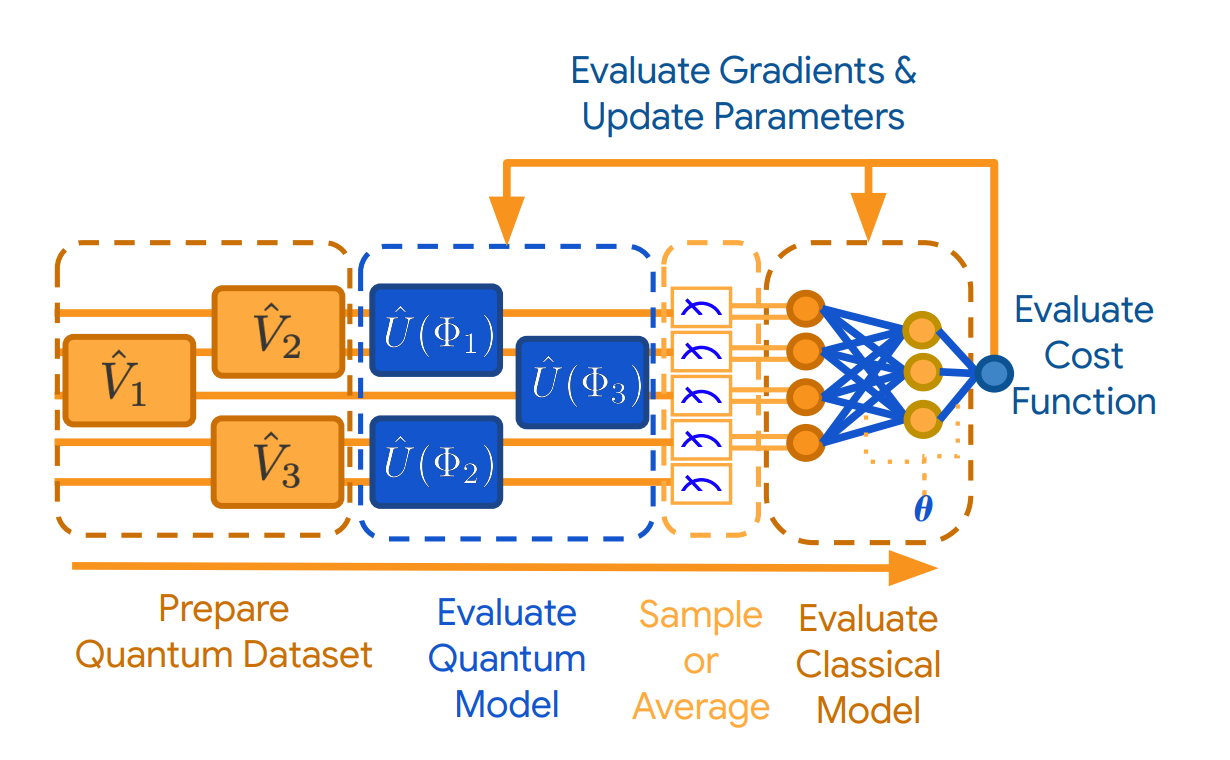
Below is a high-level overview of the the computational steps involved in a pipeline for inference and training a hybrid quantum-classical discriminative model for quantum data with TFQ:

Prepare Quantum Dataset: Quantum data is prepared using unparameterized cirq.Circuit objects and are injected into the computational graph with tfq.convert_to_tensor.
Evaluate Quantum Model: The goal of the model is to perform quantum computation in order to extract hidden information in a quantum subspace or subsystem.
Sample or Average: TFQ provides methods for averaging over several runs involving steps (1) and (2).
Evaluate Classical Model: After classical information is extracted, it is then ready for further classical post-processing. TFQ is fully compatible with TensorFlow, and quantum models can be attached to classical tf.keras.layers.Layer objects.
Evaluate Cost Function: In this step TFQ evaluates a cost function given the results of classical post-processing. Similar to traditional machine learning, the cost function may be based accuracy or classification if they are supervised, or other use other criteria if unsupervised.
Evaluate Gradients & Update Parameters: Once the cost function has been evaluated, the free parameters in the pipeline are updated in the direction expected to decrease the cost. For example, to support gradient descent, TFQ exposes derivatives of quantum operations to TensorFLow backpropagation with the tfq.differentiators.Differentator interface.

source

3. TensorFlow Quantum Primitives

In order to integrate TensorFlow with quantum computing hardware, TFQ introduced two datatype primitives:

Quantum circuit: This is a Cirq-defined quantum circuit (cirq.Circuit) within TensorFlow, which allows you to batches of circuits in varying size.
Pauli sum: This represents linear combinations of tensor products of Paul operators defined in Cirq (cirq.Paulisum)

With these two datatype primitives, TFQ provides the following operations:

Sample from output distributions of batches of circuits
Calculate the expectation value of batches of Pauli sums on batches of circuits
Simulate batches of circuits and states

You can learn more about TensorFlow Quantum design and primitives here.

3. Hello, Many Worlds

Now let's look at the first tutorial from TFQ, which:

introduces Cirq, a Python framework to create, edit, and invoke Noisy Intermediate Scale Quantum (NISQ) circuits, and demonstrates how Cirq interfaces with TensorFlow Quantum.

Installing TensorFlow Quantum

In order to install the latest stable release of TensorFlow Quantum we use the following commands in Google Colab:

!pip install tensorflow==2.1.0
!pip install -U tensorflow-quantum

Import Dependenies

Now that we have TensorFlow Quantum installed, we can import the following dependencies:

import tensorflow as tf 
import tensorflow_quantum as tfq 
import cirq 
import sympy 
import numpy as np 

# visualization tools 
%matplotlib inline 
import matplotlib.pyplot as plt 
from cirq.contrib.svg import SVGCircuit

‌Before we get into TFQ, here's an example of building a two qubit circuit with Cirq:

# Cirq uses SymPy to represent free parameters 
a, b = sympy.symbols('a b') 

# Create two qubits q0, q1 = cirq.GridQubit.rect(1, 2) 

# Create a circuit on these qubits using the parameters created above
circuit = cirq.Circuit(
    cirq.rx(a).on(q0),
    cirq.ry(b).on(q1), cirq.CNOT(control=q0, target=q1))

SVGCircuit(circuit)

Evaluating Circuits

We can evaluate circuits using the cirq.Simulator interface. We can also replace the free parameters with specific numbers by passing in a cirq.ParamResolver object:

# Calculate a state vector with a=0.5 and b=-0.5. resolver = cirq.ParamResolver({a: 0.5, b: -0.5}) output_state_vector = cirq.Simulator().simulate(circuit, resolver).final_state output_state_vector

We specify measurements in Cirq by using combinations of the Pauli operators, which are represented with a combination of $\hat{X}$, $\hat{Y}$, and $\hat{Z}$. For example, the following code measures $\hat{Z}_0$ and $\frac{1}{2}\hat{Z}_0 + \hat{X}_1$ on the state vector we just simulated:

z0 = cirq.Z(q0)
qubit_map={q0: 0, q1: 1}
z0.expectation_from_wavefunction(output_state_vector, qubit_map).real


z0x1 = 0.5 * z0 + cirq.X(q1)
z0x1.expectation_from_wavefunction(output_state_vector, qubit_map).real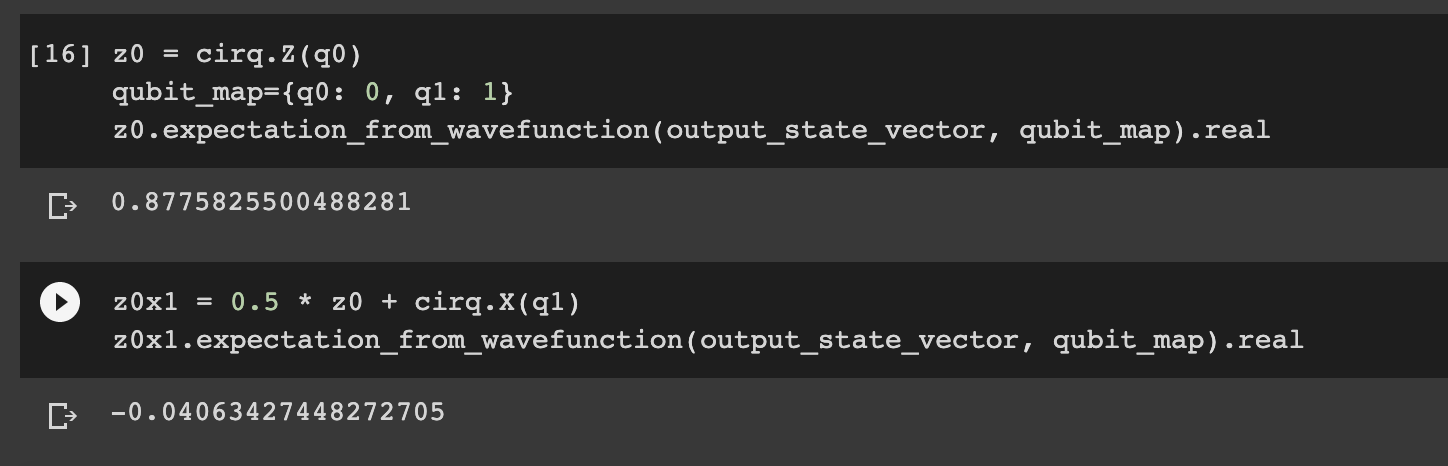

Quantum Circuits as Tensors

If we want to convert a Cirq object into a tensor we can use the TFQ function tfq.convert_to_tensor, which allows us to send Cirq objects to quantum layers and quantum ops. The function is called on lists or arrays of Cirq Circuits and Cirq Paulis:

# Rank 1 tensor containing 1 circuit.
circuit_tensor = tfq.convert_to_tensor([circuit])

print(circuit_tensor.shape)
print(circuit_tensor.dtype)

# Rank 1 tensor containing 2 Pauli operators.
pauli_tensor = tfq.convert_to_tensor([z0, z0x1])
pauli_tensor.shape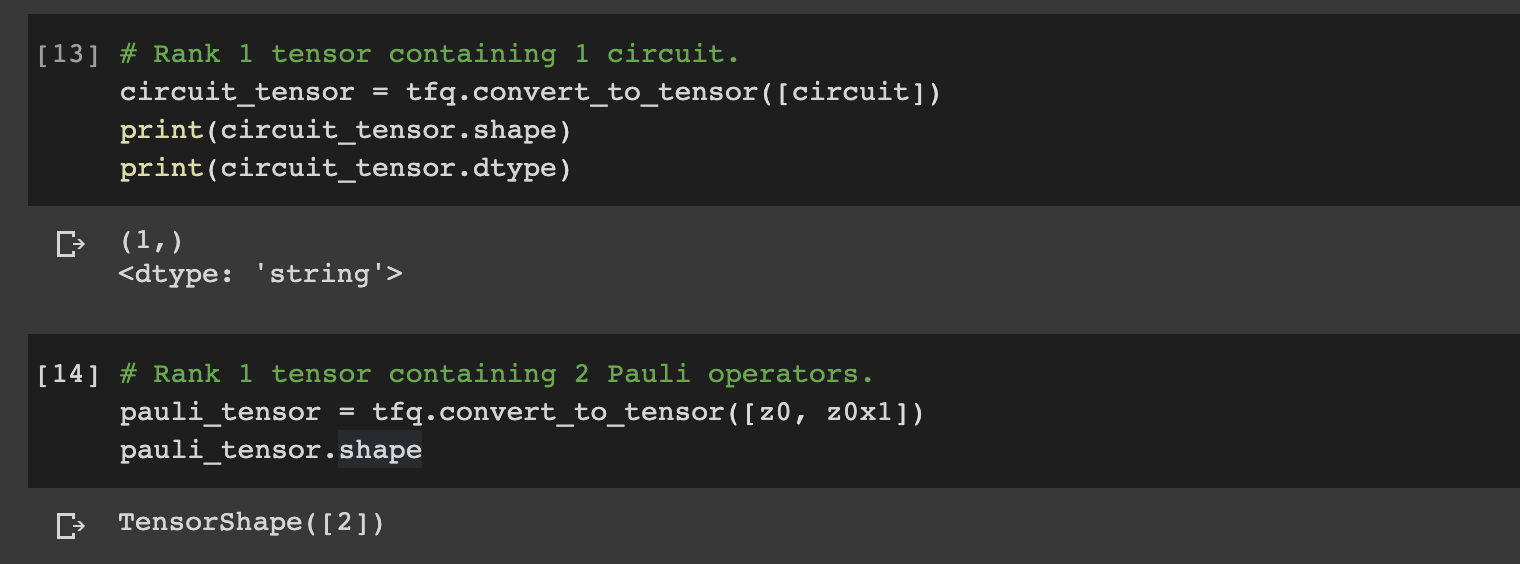

5. Quantum Machine Learning with TFQ: Tutorials

We won't cover the TFQ quantum machine learning examples in this article, although you can find links to the relevant tutorials below:

Summary: TensorFlow Quantum

As discussed, TensorFlow Quantum (TFQ) is a framework for building near-term quantum machine learning applications. TFQ allows machine learning engineers & researchers to construct quantum datasets, quantum models, and build hybrid quantum-classical ML models.