Introduction to Quantum Programming with Google Cirq

In this article we're going to take our first steps in programming a quantum computer with Google's Cirq framework.

In this article I'll assume that you have a basic understanding of quantum computers, but if you need a refresher check out these articles on the subject:

• What is Quantum Computing? Key Concepts & Industry Use Cases
• Quantum Machine Learning: Introduction to Quantum Systems
• Quantum Machine Learning: Introduction to Quantum Computation
• Quantum Machine Learning: Introduction to Quantum Learning Algorithms

This article is based on this course on quantum programming, and is organized as follows:

1. Introduction to Google Cirq
2. Quantum Hello World
3. Creating Quantum Circuits
4. Creating a Quantum Simulator with Cirq
5. The Quantum Fourier Transform Operation
6. Summary: Quantum Programming with Cirq

1. Introduction to Google Cirq

In order to program and simulate quantum circuits, we're going to make use of Google's Cirq framework, which is:

A python framework for creating, editing, and invoking Noisy Intermediate Scale Quantum (NISQ) circuits.

To get started we'll pip install cirq and then import cirq.

To check if everything is installed correctly we can check out a demo quantum circuit with print(cirq.google.Foxtail):

Now that we've got everything installed let's move on to a real quantum programming task.

2. Quantum Hello World

We're now going to define our first quantum cirquit on a quantum simulator.

To do this we'll first visualize the circuit with Quirk, which is a quantum circuit simulator:

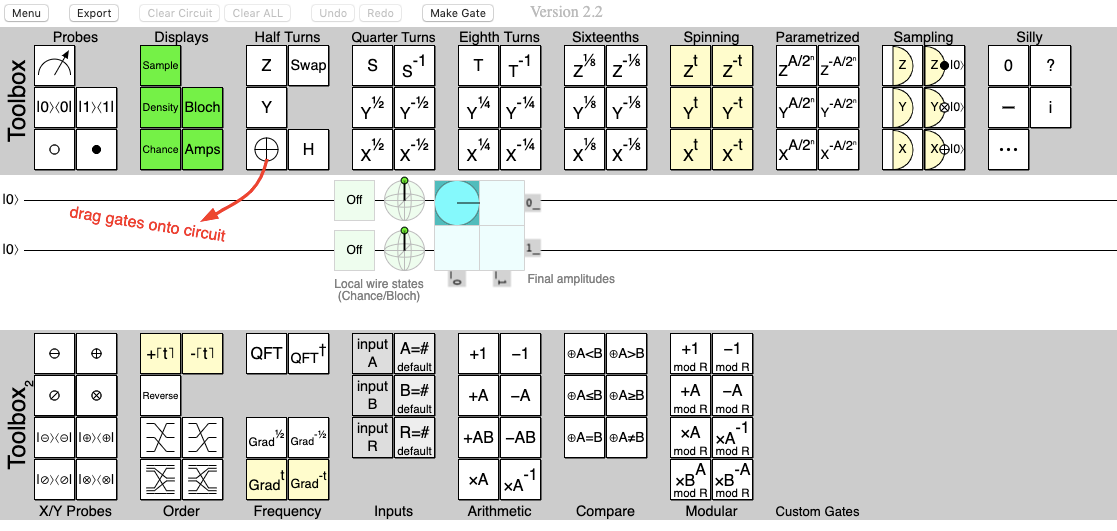
We can see we have two $|0\rangle$ qubits and we can drag gates onto these circuits, which will change the output accordingly.

Jumping back to our notebook, the first step we want to do for a basic quantum circuit is define the number of qubits, logic gates, and output.

For our qubits we use the built-in GridQubit and loop through the length two times because we want to create a 3x3 row and a column matrix.

# define the length
length = 3

# define the qubits
qubits = [cirq.GridQubit(i, j) for i in range(length) for j in range(length)]

# print the qubits
print(qubits)

Now that we've created the qubits we want to add quantum logic gates to them.

Hadamard Gate

The first quantum logic gate we'll look at is the Hadamard gate, or the H-gate.

The Hadamard gate is very important because it re-distributes the probability of the all the input lines so that the output lines have an equal chance of being a 0 and 1.

Let's go back to our simulator and drag an H-gate onto one of the $|0\rangle$ circuits:

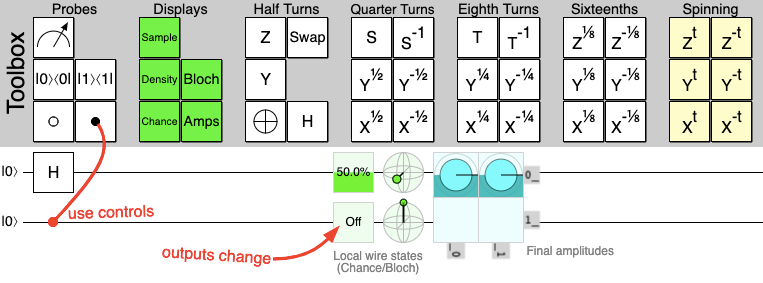
Now that we have the H-gate we can see the output has a 50% chance of being measured ON, or 1.

Let's now add an H-gate to all of the qubits in our circuit where the row + column index, or i + j, is even.

First we define a Circuit object and we are going to add to this with circuit.append.

Inside append we pass in the Hadamard gate with cirq.H(q) and loop through the qubits to check if they're even or not.

# define a circuit
circuit = cirq.Circuit()
circuit.append(cirq.H(q) for q in qubits if (q.row + q.col) % 2 == 0)
print(circuit)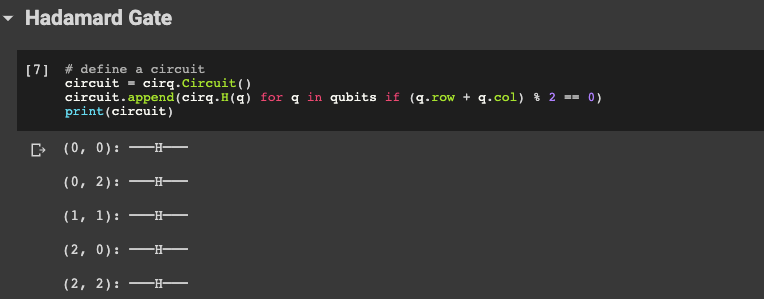

We can see we have 5 H-gates.

Pauli's X Gate

Let's now add a new gate called the Pauli X gate, which is the quantum equivalent of the NOT gate for classical computers.

A NOT gate flips the input state, so a 0 as input becomes 1 as output, and vice versa.

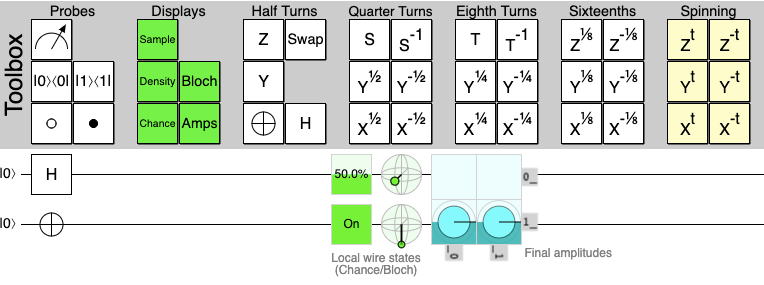
We can see the output of our $|0\rangle$ circuit has is now ON, so the chance of measuring a 1 is 100%, and if we add another Pauli X gate our output becomes OFF.

Let's noww add a Pauli X gate to our cirq circuit.

circuit.append(cirq.X(q) for q in qubits if (q.row + q.col) % 2 == 1)
print(circuit)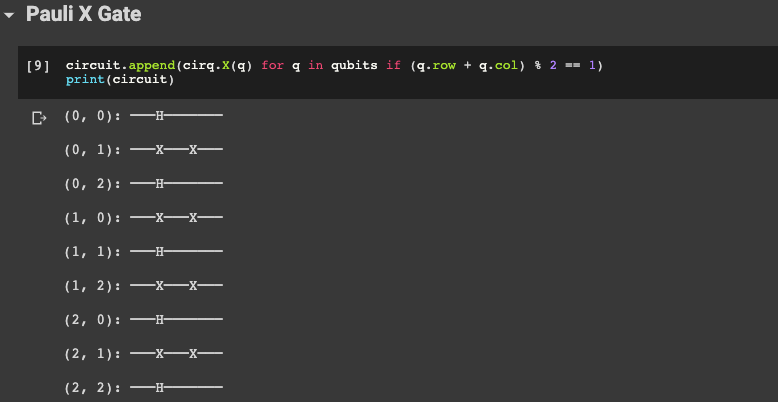

Let's now look at how a quantum circuit is represented in Cirq.

A Cirq Circuit is made up of group of Moments, and a Moment is made up of a group of operations.

If we look at our Pauli X gate above one issue is that the H-gates and the X-gates get executed at different times.

Instead, we want both the H and X gates to be executed at the same time.

So what we're looking for is to have one Moment with both the H and X-gates.

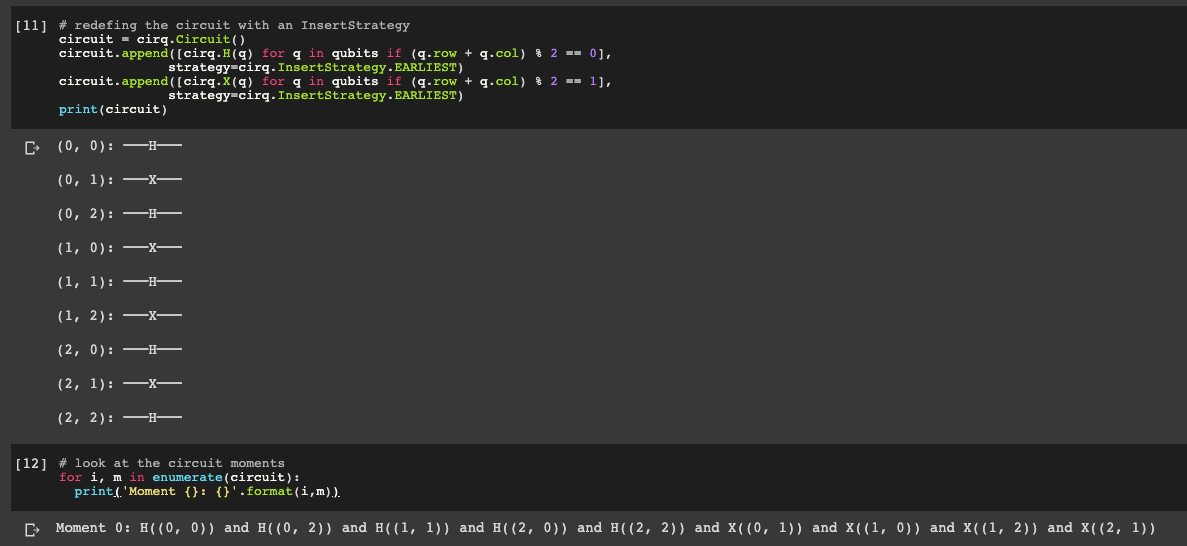
To make sure we only have one Moment we're going to set our strategy equal to cirq.InsertStrategy.EARLIEST, which governs the time of the operation execution.

# redefing the circuit with an InsertStrategy
circuit = cirq.Circuit()
circuit.append([cirq.H(q) for q in qubits if (q.row + q.col) % 2 == 0],
              strategy=cirq.InsertStrategy.EARLIEST)
circuit.append([cirq.X(q) for q in qubits if (q.row + q.col) % 2 == 1],
              strategy=cirq.InsertStrategy.EARLIEST)
print(circuit)

# look at the circuit moments
for i, m in enumerate(circuit):
  print('Moment {}: {}'.format(i,m))

Now we can see we only have one Moment in the Circuit.

3. Creating Quantum Circuits

As mentioned, a Circuit is defined as a set of Moments.

A Moment is defined as a set of operations that can be executed on Qubits.

So to create new Circuits we need to create new Moments, which we can do with cirq.moments().

Here's what we're going to do:

• We're first going to define our grid of qubits
• We then apply an X-gate at Qubit location (0,0)
• We then turn it into an operation
• We then define new Moments
• We the combine Moments together to create a new circuit

# creating a grid of qubits
qubits = [cirq.GridQubit(x, y) for x in range(3) for y in range(3)]
print(qubits)

# applying a gate at Qubit location (0,0)
x_gate = cirq.X

# turn in into an operation
x_op = x_gate(qubits[0])
print(x_op)

# define a Moment
cz = cirq.CZ(qubits[0], qubits[1])
x = cirq.X(qubits[2])
moment = cirq.Moment([x, cz])
print(moment)

# define a Circuit by combining Moments togeteher
cz01 = cirq.CZ(qubits[0], qubits[1])
x2 = cirq.X(qubits[2])
cz12 = cirq.CZ(qubits[1], qubits[2])
moment0 = cirq.Moment([cz01, x2])
moment1 = cirq.Moment([cz12])
circuit = cirq.Circuit((moment0, moment1))
print(circuit)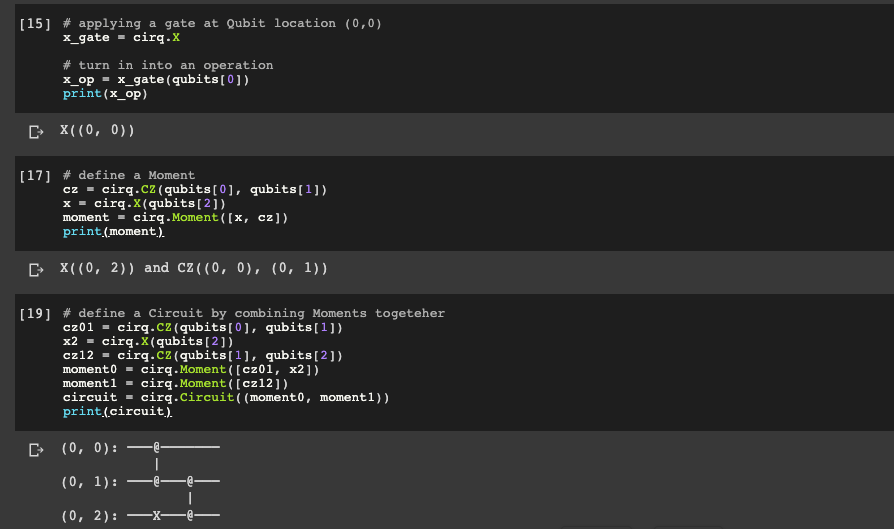

Insert Strategies

Let's now look at InsertStrategy class in a bit more detail, you can find the documentation for it here.

There are a few different types of InsertStategy attributes we can use to create a quantum circuit with Cirq.

Insert strategies can help the execution of the circuit and can make the creation of new Moments easier.

As we've discussed whenever we create a quantum circuit there are 3 main tasks:

1. Define the initial qubit state
2. Define the operations and Moments
3. Measure the output

InsertStrategy is a crucial part of the second step when we add new operations on to Moments.

Let's look at an example:

• We're first going to import the CZ and H gates from cirq.ops and ImportStrategy from cirq.circuits
• We're then going to define 3 qubits with cirq.GribQubit

from cirq.ops import CZ, H
from cirq.circuits import InsertStrategy
q0, q1, q2 = [cirq.GridQubit(i, 0) for i in range(3)]

Next let's look at InsertStrategy.EARLIEST, which adds the operation onto the very first Moment.

circuit = cirq.Circuit()
circuit.append([CZ(q0, q1)])
circuit.append([H(q0), H(q2)], strategy=InsertStrategy.EARLIEST)
print(circuit)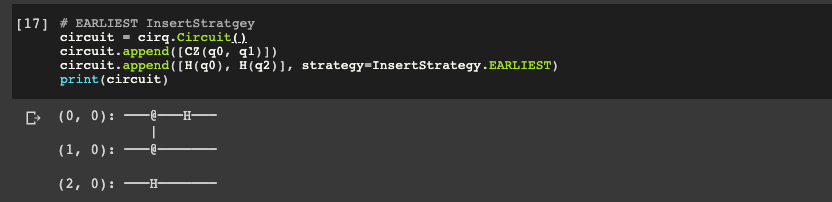

We can see the H-gate is inserted on the first Moment of the circuit.

Next let's look at InsertStrategy.NEW, which creates a new Moment and adds the operation to it.

circuit = cirq.Circuit()
circuit.append([H(q0), H(q1), H(q2)], strategy=InsertStrategy.NEW)
print(circuit)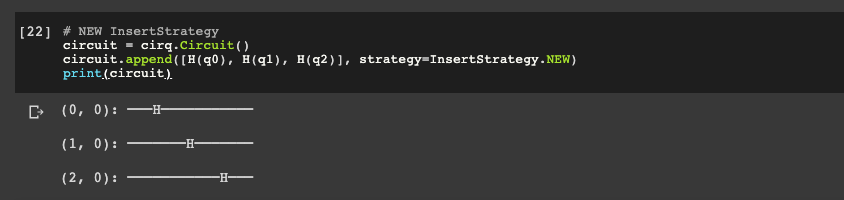

Next let's look at InsertStrategy.INLINE, which adds operations in a Moment a specific instant.

circuit = cirq.Circuit()
circuit.append([CZ(q1, q2)])
circuit.append([CZ(q1, q2)])
circuit.append([H(q0), H(q1), H(q2)], strategy=InsertStrategy.INLINE)
print(circuit)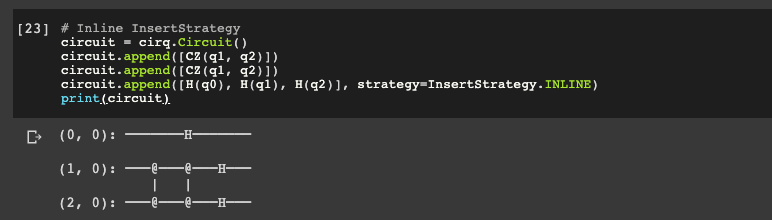

Finally let's look at InsertStrategy.NEW_THEN_INLINE, which as the name suggests is a combination of the NEW and INLINE strategy.

circuit = cirq.Circuit()
circuit.append([H(q0)])
circuit.append([CZ(q1, q2), H(q0)], strategy=InsertStrategy.NEW_THEN_INLINE)
print(circuit)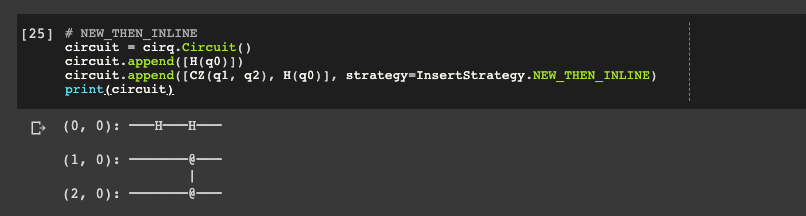

Now that we've created quantum circuits, let's create a simple quantum simulator with Cirq.

4. Creating a Quantum Simulator with Cirq

Let's now use Cirq to simulate quantum phenomenon on a classical computer.

Cirq has a built-in package for a quantum simulator, which displays the corresponding output based on the circuit provided.

For this example, we're going to simulate 2 qubits:

q0 = cirq.GridQubit(0,0)
q1 = cirq.GridQubit(0,1)

Now that we've declared our qubits we want to declare a basic_circuit, a method for the circuit model:

# create a basic circuit constructor
def basic_circuit(meas=True):
  sqrt_x = cirq.X**(0.5)
  yield sqrt_x(q0), sqrt_x(q1)
  yield cirq.CZ(q0, q1)
  yield sqrt_x(q0), sqrt_x(q1)
  if meas:
    yield cirq.measure(q0, key='alpha'), cirq.measure(q1, key='beta')

We then define a new circuit and append our basic_circuit method to it:

circuit = cirq.Circuit()
circuit.append(basic_circuit())
print(circuit)

Now let's run this circuit with the Cirq simulator:

from cirq import Simulator
simulator = Simulator()
result = simulator.run(circuit)
print(result)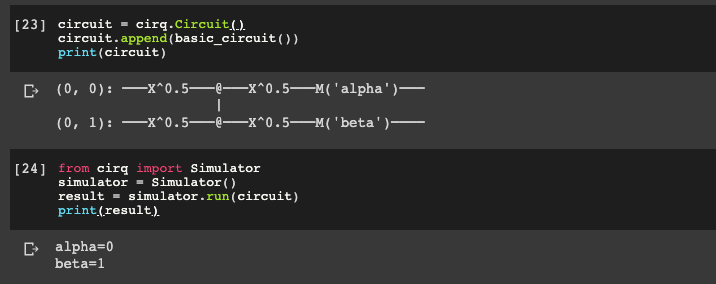

5. The Quantum Fourier Transform Operation

Now let's move on to our first real project and create the quantum Fourier transform circuit and simulate it with Cirq.

Here's a brief summary of a Fourier transform:

The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of time.

In simpler terms, a Fourier transform converts a single energy distribution into its constituent energy.

For example, a musical chord can be expressed in terms of the volume and frequencies of the constituent notes.

Let's now extend this concept to a quantum circuit, here's the definition of a quantum Fourier transform:

The quantum Fourier transform is the classical discrete Fourier transform applied to the vector of amplitudes of a quantum state, where we usually consider vectors of length $N :=2$.

This is similar to the Hadamard gate which redistributes the entire energy distribution, except the quantum Fourier transform is distributed according to the initial energy distribution.

The quantum Fourier transform can also be seen as a way to convert data, which is encoded with frequency, and convert it into a phase representation.

A phase refers to a part of the whole, so if we have a complete phase we've completed an entire cycle.

In this example we're going to use 8 qubit states, so we will encounter a phase distribution that is divided into 8 parts.

To summarize, Fourier transform is a redistribution of energy, so when you have an output you can decode the inputs from it.

Let's now implement a quantum Fourier transform circuit with Cirq.

Defining the Hadamard Gate

• We're first going to define a main() method for our app
• Inside the main() method we're going to create a basic circuit with 4 qubits qft_circuit
• We create the 4 qubits with our generate_2x2_grid() method and then define the Circuit
• Inside the Circuit we pass in the operations that will be used for to create the circuit, which are a series of Hadamard operation H(a) and then the CZ swap operations cz_swap on the qubits
• We then pass in the InsertStrategy.EARLIEST as the strategy and then return the circuit
• We're then going to create a simulator, pass in the qft_circuit and print the final result using numpy

import numpy as np
import cirq

def main():
    qft_circuit = generate_2x2_grid()
    print("Circuit:")
    print(qft_circuit)

    # creating a simulator
    simulator = cirq.Simulator()

    # pass in the circuit and print the result
    result = simulator.simulate(qft_circuit)
    print()
    print("Final State:")
    print(np.around(result.final_state, 3))

def cz_swap(q0, q1, rot):
    yield cirq.CZ(q0, q1)**rot
    yield cirq.SWAP(q0, q1)

def generate_2x2_grid():
    a,b,c,d = [cirq.GridQubit(0,0), cirq.GridQubit(0,1), cirq.GridQubit(1,1),
                cirq.GridQubit(1,0)]
    circuit = cirq.Circuit.from_ops(
        cirq.H(a),
        cz_swap(a, b, 0.5),
        cz_swap(b, c, 0.25),
        cz_swap(c, d, 0.125),
        cirq.H(a),
        cz_swap(a, b, 0.5),
        cz_swap(b, c, 0.25),
        cirq.H(a),
        cz_swap(a, b, 0.5),
        cirq.H(a),
        strategy=cirq.InsertStrategy.EARLIEST,
    )
    return circuit


if __name__ == '__main__':
    main()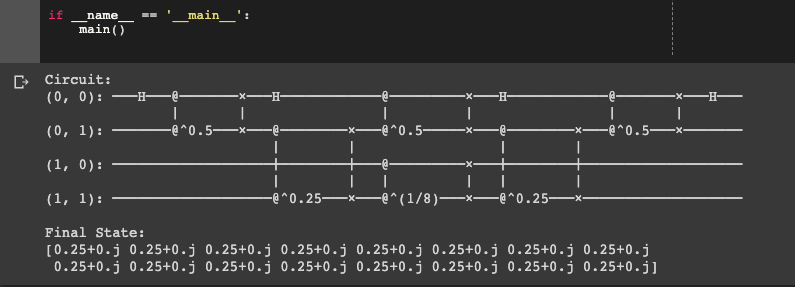

We've now created a quantum Fourier circuit. We can now build off this algorithm to create a quantum annealer, but we'll save that for another article.

6. Summary: Quantum Programming with Cirq

In this article we looked at how to program and simulate quantum circuits with the Google's Cirq framework, which is:

A python framework for creating, editing, and invoking Noisy Intermediate Scale Quantum (NISQ) circuits.

We started by learning how to define qubits and then add quantum operations to them. We looked at several quantum gates including the Hadamard gate and Pauli's X gate.

We then discuss how to create quantum circuits. In Cirq, a Circuit is defined as a set of Moments, and a Moment is defined as a set of operations that can be executed on qubits.

We then looked at how to create a quantum simulator with Cirq.

Finally we tied all of this together by creating a quantum Fourier transform circuit and simulating in with Cirq.

In the next article we'll build on these concepts and look at programming a quantum annealer with D-Wave.

Resources

• Quantum Computing: Theory to Simulation and Programming